There is a great deal about digital audio that is counter-intuitive. And perhaps the strangest notion in the field is that noise is good!

Sounds strange, huh? After all, even the now-ancient 16 bit standard of the CD gives a theoretical noise floor of -96dB, so why would you want to raise the level of the noise? The reason is that an appropriate amount of noise kills some kinds of digital distortion.

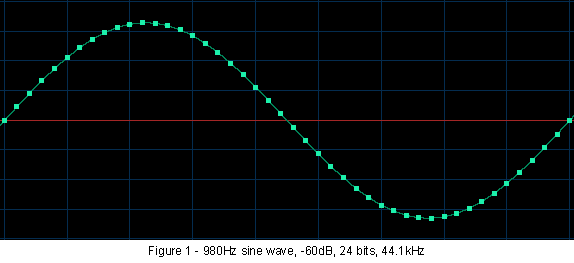Here I shall illustrate this with pictures. But first, the background. A PCM (Pulse Code Modulation) digital signal of the kind used on CDs and DVD Audio records an analogue signal by measuring the instantaneous level of the signal regularly and storing the result. Figure 1, for example, shows what this looks like. The thin green line shows what would be the original analogue signal had I actually recorded it (I didn't, all the signals in this article were digitally generated and remained in digital domain the whole time until converted by your computer into an analogue signal for your monitor.) The little green boxes superimposed on this line are important. Notice how they're evenly spaced horizontally? The horizontal axis is time. Each box shows the level of the analogue signal at that instant. Each box is called a 'sample'.

A PCM recording is simply a long list of the values of those boxes. Two important determinants of the accuracy of that recording are how frequently those values are recorded, and the degree of resolution that the numbering system allows. The signal in Figure 1 uses the CD-standard sampling frequency of 44,100 hertz. That means that 44,100 samples are taken each second. The waveform shown is a 980 hertz sine wave. If you count up the number of samples in one full cycle, you will see that there are 45. Divide 44,100 by 45 and you get 980. (I use 980 hertz here rather than 1,000 simply because 1,000 does not divide evenly into 44,100, and when you start manipulating the signal it generates all sorts of spurious noises.)

Since this is digital technology, it uses a binary number to record the value of each sample. In digital audio there are three choices: an eight bit number, a 16 bit number and a 24 bit number. The total range of values that can be held by an 8 bit number is determined by raising 2 to the power of 8 (that is, multiplying 2 by itself eight times). This yields a mere 256 different values. Thankfully 8 bit digital audio is largely obsolete (except for the sounds provided with some computer applications).

By contrast, a 16 bit recording can use a number space with 65,536 different levels to record the momentary level of the analogue signal. 24 bits allows even more precise recording, with around 16.7 million levels.

Recording 16 bits

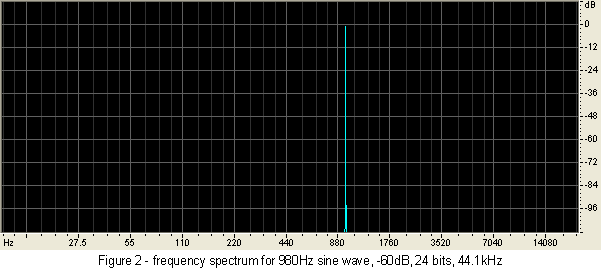
Now let's go back to Figure 1. This 980 hertz sine wave was created to simulate a very quiet sound in a recording. Its peak level is 60 decibels below the maximum recording level (that is: -60dBFS where FS is 'Full Scale'). Despite this it sounds excellent, because I cheated. I created this test signal with a resolution of 24 bits. See Figure 2, which shows the frequency spectrum of this signal. The 0dB mark on the right hand axis is actually displaced to indicate -60dBFS. Yet even at the bottom of the figure (which is at -168dB full scale) there is no noise showing. Ah, digital perfection!

Now let us simulate recording this signal on a 16 bit system. Actually, I will do a digital conversion from 24 bits to 16 bits. Note that this is a 'pure' conversion, with no other processing. All that will happen is that the computer recalculates the height of each sample from a 24 bit number space, down to a 16 bit number space, while retaining the same overall level (that is, -60dBFS for the peaks). Figure 3 shows the frequency spectrum of the result.

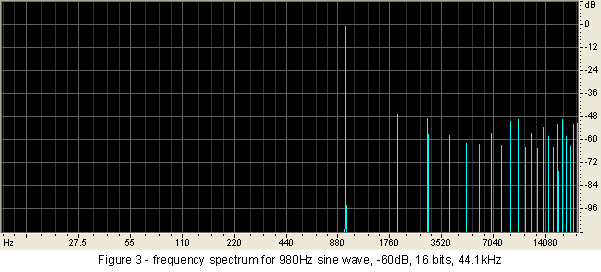Oh, horrible, horrible digital! Look at all those spikes at the right hand end. A close examination of the horizontal axis shows that they are harmonics of the 980 hertz fundamental, and all at horribly high levels. Worse, rather than rapidly diminishing as the order increases (which is the norm for natural sounds), the level is roughly maintained through to the 22nd harmonic!

In fact, the total harmonic distortion, with reference to the -60dBFS 980 hertz fundamental, is an appalling -39dB, or 1.1%. If this were all second and third harmonic, it would be acceptable, but the spread into the high frequencies makes it completely unacceptable.

What has gone wrong?

Let us go briefly back to the original 980 hertz tone. This was created with a peak level of -60dB but with 24 bits of resolution. The highest sample value out of the roughly +/-8 million available was 8,389 (there are another 8+ million below zero, adding up to the 16.7 million total). This value is just slightly higher than can be held by a 14 bit number space, so the original signal had an effective resolution of 14 bits. But after conversion to 16 bits, which involves scaling down each sample by a factor of 256, the highest sample value is a mere 33. This is very slightly better than 5 bit sound. Now look at Figure 4, which shows the top portion of the resulting wave. See how the top three samples of the peak are all on the same line? Well, they can't be between the lines because there are no valid values there.

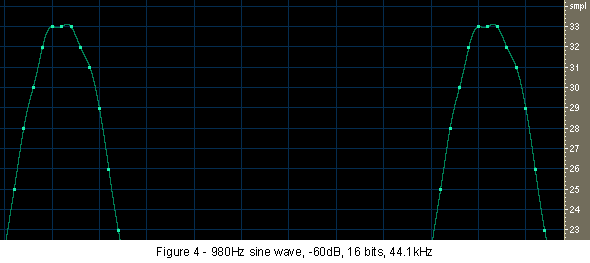That stepped waveform generates heaps of harmonics. When I played back this signal on my headphones, turned up nice and loud, the sine wave was very harsh indeed, with some of the harmonics clearly audible ... and irritating.

Noise to the rescue!

This is where 'dither' noise comes in. At the last stage in preparing audio for CD, an extremely low level of noise is added to the signal. This noise is typically achieved simply by randomising the least significant bit of the each sample: that is, randomly adding either zero or one to this bit. This produces a peak noise level of -90dBFS, and an average noise level of -93dBFS, and the character of the noise is 'white'. You are going to have to be playing your CD very loud indeed in a very quiet room to hear this!

But by randomising this least significant bit, it also removes the regularity from the errors in the actual signal. Remember, at least the same number of (and perhaps even more) errors remain, but they are now random errors instead unfortunately repeating steps along the edge of a sine wave. What this does, in turn, is eliminate the harmonics.

This does not sound very intuitive at all, so let us prove the point. I go back to my original -60dBFS 980 hertz signal with 24 bits of resolution and again reduce it to 16 bits. But this time I add a one bit level of dither during the conversion. The frequency spectrum of the result is shown in Figure 5. Two things immediately stand out. First, there is a significant noise floor at -78dB (-138dBFS). Second, there are no harmonic spikes. These haven't just been masked (look again at Figure 3: they read up to 30dB above where the new noise floor has been placed). They have been eliminated!

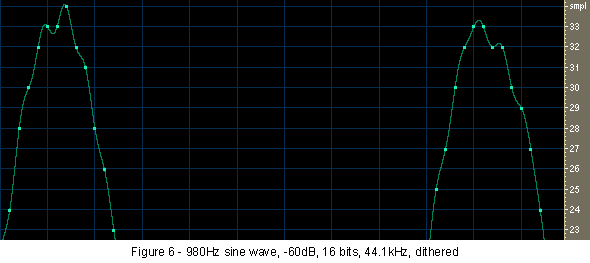
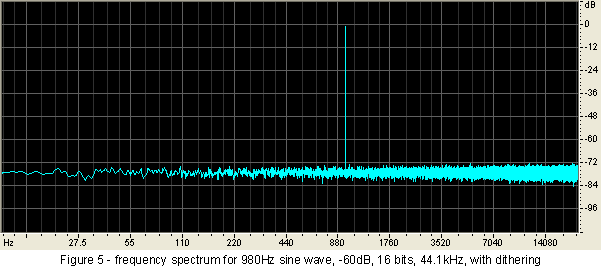Have we smoothed the waves? Not in the slightest. Look at Figure 6, where I've zoomed in on the top of two of the resulting cycles. If anything, the waves are even bumpier than they were in Figure 4. But now the bumps are in different places on each cycle. Similarly, by filtering out the 980 hertz fundamental I measured and calculated the average noise level to be a mere 30dB below the -60dBFS signal, or somewhat higher than the average total harmonic distortion.

Nevertheless, white noise at -93.3dBFS (which is what this was) is rarely audible, and certainly less objectionable, than high order harmonic distortion.

There was no magic here. Just a mathematical conversion of high levels of regular (and irritating) harmonic distortion, which was concentrated into some very narrow parts of the frequency spectrum, into a low level of far more tolerable white noise which is spread across the whole spectrum. More succinctly, we've just pushed down those objectionable spikes into the ground which, in turn, has risen a bit. But the ground is now flat and far less likely to be tripped over.

Moving the noise to where it does the least harm

Once again, you don't get something for nothing. The idea here is simply to move some of the noise from one part of the audio spectrum to another. Ideally you would reduce the noise levels significantly across the audio band, and shove it all up above 20,000 hertz where it is relatively, perhaps totally, inaudible. In practice, on a CD there is only a very small window between 20,000 hertz and the 22,050 hertz cut off, so there are limits to what can be done. Still, a fair bit can indeed be done.

So let's repeat the process from the start, but this time instead of adding standard dither noise, we'll add dither noise that has been shaped optimally for a 44,100 hertz sampling frequency.

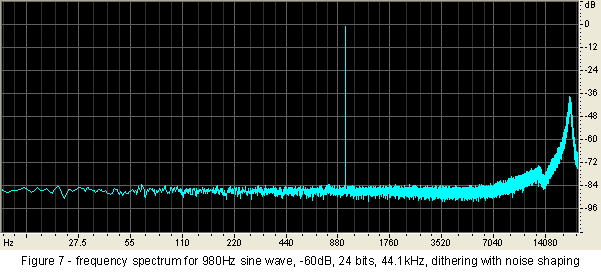
The result is shown in the frequency spectrum shown at Figure 7. Compare this to the non-shaped noise in Figure 5. Instead of the noise hovering around -78dB (ref the -60dBFS signal), it has descended to around -87dB, a 9dB improvement. The tradeoff for this improvement is that it only covers the frequency band up to around 7,000 hertz, whereupon the noise floor starts to rise to a quite poor -42dB (ref the -60dBFS signal) at just under 20,000 hertz.

But, remember, our ears are very much more sensitive in the midrange and low treble than they are in the high frequencies, and it is this characteristic upon which noise shaping relies to deliver a perceived improvement in overall performance.

Conclusion

Interesting and somewhat controversial questions, these. My take on it is 'no' to both of them.

For the first question, there are some things that ought to be taken into account. Many recordings already have quite sufficient dither within them. The tape hiss on analogue recordings, even if heavily supressed with Dolby Noise Reduction, serves this purpose, as does the residual noise from some microphone preamplifiers and even, in some cases, microphones themselves.

Yet even where ultra-low noise microphones and electronics are used, dither may not be necessary at the tail end of the CD production process (although it could be at some stages within mixing, if some of the source material is already 16 bits in resolution and has to be increased in level). In the case examined above, the THD was -39dB, but that was with reference to a signal that was itself -60dBFS. Now if a CD has been normalised so that the peaks reach 0dBFS, then that distortion level will be -99dBFS, or 99dB below the peak playing level. If you are running a good system loud you might get the odd 110dBSPL peak, while the THD level would be at just 11dBSPL. The individual distortion components, themselves reaching to no more than -49dB (ref the -60dBFS tone), would actually be below the limits of human hearing in even a perfectly silent environment.

As to dithering high resolution recordings, why bother? Even generating a 980 hertz tone with a peak level of -120dBFS in a 24 bit environment produces distortion components that are discernible neither visually nor audibly. For that matter, I doubt that there is any equipment outside of an experimental laboratory that could reproduce that tone significantly above the level of equipment noise.

© 2003 by Stephen Dawson