(Originally published in Australian HI-FI Magazine, March/April 2015, Volume 46 No 2)
Digital audio is not a subject lending itself to intuitive human understanding. But we try to use words best suited to such understandings to describe it. Unfortunately, it too often leads us astray.
So we have arguments between audiophiles and engineers on the value — even the audibility — of different forms of digital audio. Is DSD better sounding than PCM, or is it merely a different way of representing a digital signal of a certain resolution? Does an increase in the PCM sampling frequency from 44.1kHz to 96kHz, or even to 192kHz, yield audible improvements? If so, how are they manifested? Is the increased resolution of 24 bit audio worth the doubling in file size*?
How do you even judge these things?
A good start is by gaining a strong understanding of what audible effects these things can actually have on music. But that can be difficult. Most people would accept that the difference in quality between 16 bit and 24 bit PCM sound is likely to be subtle, so it can be difficult to put your finger on what the precise difference is, if any.
Being human, our judgements about these things can be influenced by how we conceptualise them. But, as I stated at the outset, digital audio is not easily intuitive. So we might think in analogies. Sixteen bit PCM defines sound on a scale with 65,536 levels. With 24 bits that goes to 16,777,216 levels. It is tempting to think that the latter is going to sound smoother than the former, since each sample is more precisely defined. Surely 16 bits will sound ‘grainier’, by analogy with course beach sand vs the fine talc of 24 bits.
And it should sound even grainier still if you drop down even further to a mere eight bits. That, after all, encodes each sample to one of just 256 levels! Perhaps pebbles, rather than grains.
We all know eight bit sound is awful. Or, at least, those of us old enough to remember the system sounds on Windows 95 (and earlier) computers, many of which were just 8 bits (and often 22.05kHz or lower in sampling frequency). But how bad, and bad in what way, is determined by more than just the bit depth. The sound can be treated — even 8 bit sound — to make is much better than you might expect.
Let’s illustrate this. I’m using the final 13 seconds of the track ‘Kangaroo Street, Part 1’ from the album Walk into the Sun by the Sydney group B’Jezus (thanks to Jez Ford, editor of sister magazine Sound+Image, and leader of the group, for permission to use the track**). This is of course in standard CD quality — 16 bits, 44,100 hertz sampling — and the section consists of a final refrain followed by a nicely natural acoustic fade out. I added one second of digital silence at the start to allow time for DACs to lock on. Then I did a straight conversion to 8 bits. No changes other than that, and with no dither added.
Listening to this is fascinating. For the first second there’s still no sound, because digital black in 8 bits is identical to digital black in 16 bits. But the instant the actual signal starts a background noise becomes obvious. For the first six or seven seconds it sounds more or less like white noise in the background of music that otherwise sounds the same as the original. But as the music quietens, particular during the decay of the gently plucked guitar strings, there is a distinct static-like feel, and the final decay of the guitar sounds like it has been placed in a fast modulation envelope, something which is definitely not there in the original.
This is the sum total of what happens when music is naively reduced in resolution. First, there is white noise. Second, there can be artefacts associated with low levels of signal. With 8 bits of resolution, any parts of the signal below -48dB will be encoded at either one or zero bits of resolution, effectively as square waves. That will both generate odd order harmonics and in the case of repeating tones, emphasise the fundamental so that it peaks at -48dB.
So what can we do about it? Dither is the answer! Dither is low level noise that is added to the signal. This has the effect of removing correlations and breaking up artefacts. The cost is that the level of white noise is raised. So the signal itself is just as pure as the original higher resolution one, but it is immersed in a fair bit of noise.
So what can we do about that? Noise-shaping is the answer! Basic dither just randomises the least significant bit of the signal — it randomly adds, or doesn’t add, one. Noise shaped dither is noise which is stronger in some frequency bands than in others. There are plenty of shapes available, but the one that suits our purposes is to lower noise in the most audible part of the spectrum at the cost of increasing it in less audible parts. For this purpose I chose an aggressive one called E2 in my software, with a nominal 1 bit of depth. All the noise below about 11kHz is lower than with plain dithering, over 24dB lower at 1kHz. But above 15kHz the noise is much louder. Listening-wise, it is far less objectionable and leaves the music much clearer. Fine tuning with different noise shaped curves and reduced levels of dither can improve the results further.
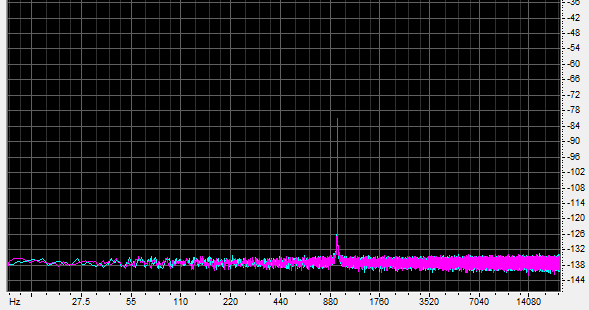
The graphics illustrate these shapes. The first shows the spectrum of a 980Hz sine wave of -80dB recorded (digitally created, actually) in 16 bits.
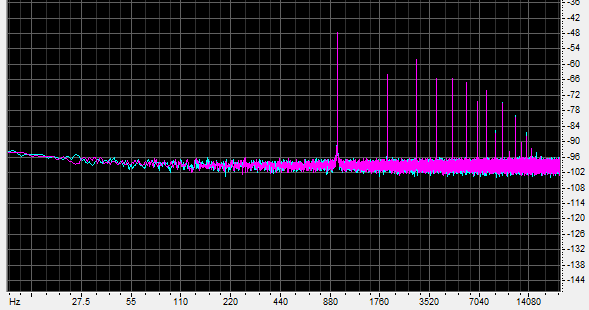
The next shows a naive down-conversion to 8 bits (ie. with no added dither):
You will notice that not only has the noise floor increased from -136dB to -100dB, there are massive amounts of harmonic distortion, even out to the fifteenth harmonic. Even more disturbingly, instead of being at -80dB, the main tone is at -48dB and most of the distortion components are also higher in level than the fundamental itself is supposed to be! Play this loud and the 980 hertz tone sounds way too loud, and rather like a square wave, thanks to the harmonics.
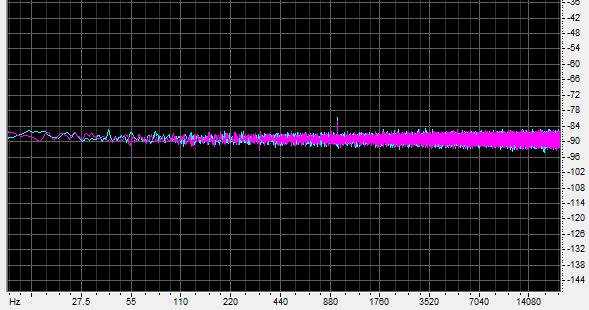
Once we add dither, proper order is restored:
The harmonics disappear and the 980 hertz tone resumes its proper level. But the noise floor is now at -88dB, an increase of 12dB. The tone is only 8dB higher than the noise, and I was unable to hear it when I turned up the volume.
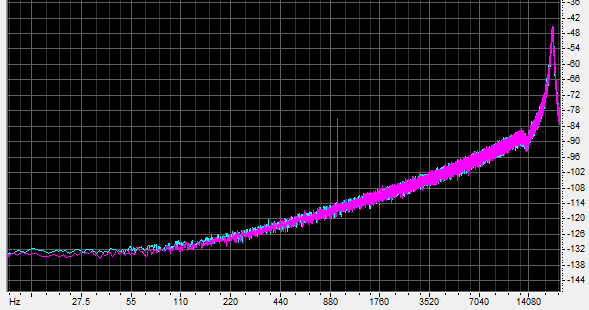
Finally, with the E2 noise shaped dither:
The 980 hertz tone is still at the proper level, still undistorted, but at least 30dB above the noise floor in its frequency band. In the band of frequencies to which the ear is most sensitive, the noise is greatly lowered. The tone was audible and clean with the volume advanced.
Let’s pause for a moment. This sine wave peaks at -80dB, which is 32 decibels below what you’d expect to be the resolving ability of 8 bit PCM. Yet with some shaped dither — the addition of some artificial noise — it is clear and clean.
More important than the pictures, though, is listening with your own ears. The four versions of the excerpt, and the four versions of the -80dB 1kHz tone, can be downloaded from my blog post on the subject ‘The Magic of Dither‘ (where I also explain why the 980Hz signal was made too loud by the undithered 8 bit conversion) or from AV Hub. You might be surprised that the 8 bit version with noise shaped dither is almost listenable, and does not sound at all like what most people’s preconception of 8 bit audio should sound like.
So when assessing 16 bit versus 24 bit sound, you know what to listen for. Just remember the noise will be 48dB quieter, and any artefacts in undithered material will not only be 48dB quieter, they will also be much rarer since much less content is encoded to less than -96dB than there is to -48dB.
—-
* In the real world, lossless compression is much less efficient with the additional eight bits than with the most significant sixteen, because the additional bits mostly encode noise.
** If you like the music, why not purchase/download it?